壓縮原理算法
使用C實現壓縮演算法及其原理
RunLength
- 簡單來說,RunLength想法就是將遍歷數據統整出現次數和該值再重新寫入
- RunLength 有3種,其中又為第3種最常運用在BMP圖像格式以及PCX等資料格式也會使用這種方法
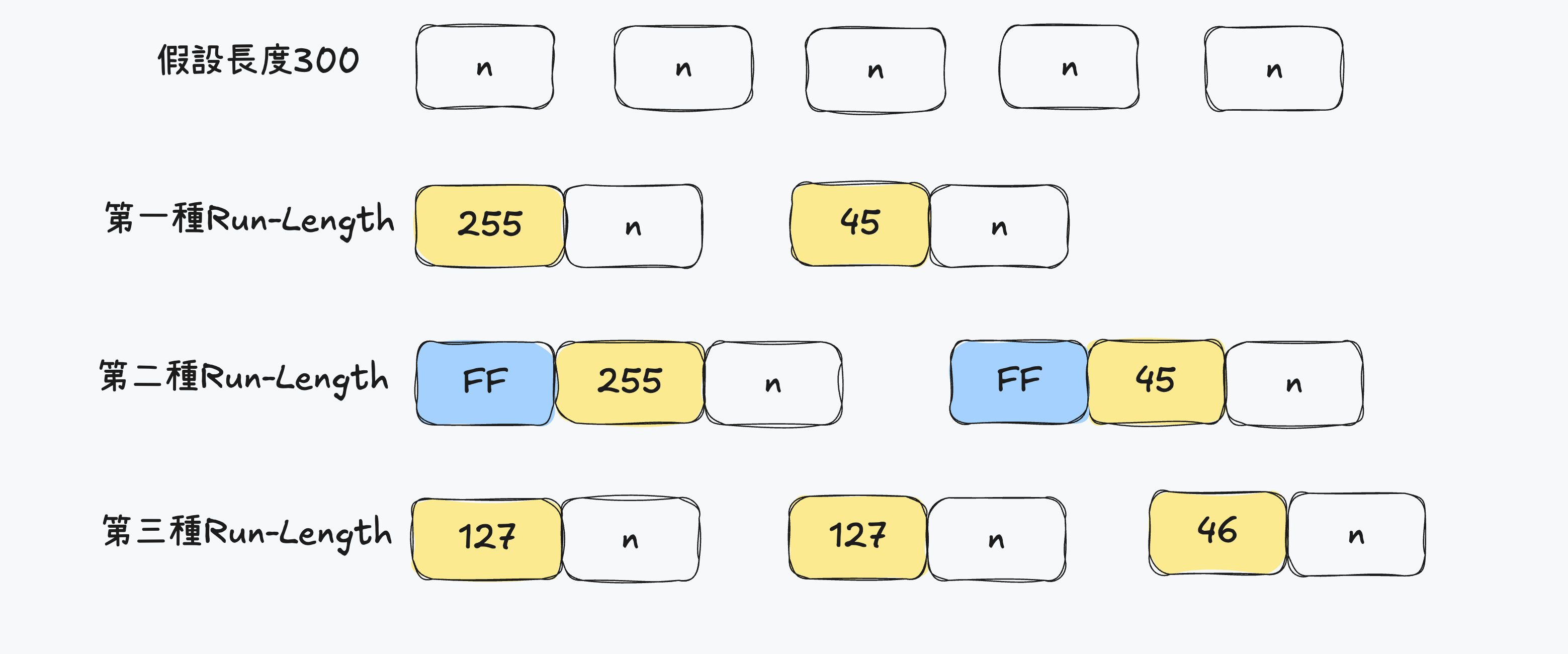
- 基本的RunLength編碼
- 插入表示RunLength的碼
- 將長度部分作為表示RunLength的碼
公用函數
讀取準備壓縮文件
#define BUFFER_SIZE 102400
typedef unsigned char byte;
unsigned char buffer[BUFFER_SIZE];
int main(const int argc, char *argv[])
{
int c;
if(argc < 3) {
exit(8);
}
FILE *fp_i = fopen(argv[1], "rb");
if(fp_i == NULL) {
fprintf(stderr, "Input file cannot open \n");
exit(8);
}
int i = 0;
while(i<BUFFER_SIZE && (c = fgetc(fp_i)) != EOF) {
buffer[i] = c;
i++;
}
fclose(fp_i);
FILE* fp_o = fopen(argv[2], "wb");
if(fp_o == NULL) {
fprintf(stderr, "Output file cannot open \n");
exit(8);
}
encode(fp_o,buffer,BUFFER_SIZE);
fclose(fp_o);
return 0;
}讀取準備解壓縮文件
int main(int argc,char **argv) {
FILE* fp;
if ((fp=fopen(argv[1],"rb")) == NULL) {
fprintf(stderr,"Can't open file %s\n",argv[1]);
exit(1);
}
decode(fp);
fclose(fp);
return 0;
}獲得資料長度
int getRLE(byte *img,int x,int mx,int lim,int *run,int *code) {
int px = 0;
px = x;
*run = 1;
*code = img[px];
px++;
while (px < mx && *code == img[px] && *run < lim) {
px++;
(*run)++;
}
return px;
}
RunLength壓縮算法
第一種壓縮
int encode(FILE *fp,byte *img,int mx) {
int run,code;
int x = 0;
while (x < mx) {
x = getRLE(img,x,mx,0xff,&run,&code);
fputc(run,fp);
fputc(code,fp);
}
return 0;
}
第一種解壓縮
int decode(FILE *fp) {
while (!feof(fp)) {
int run = fgetc(fp);
int code = fgetc(fp);
for (int i=0; i<run; i++) {
fputc(code,stdout);
}
}
return 0;
}第二種壓縮
int encode(FILE *fp,byte *img,int mx) {
int run,code;
int x = 0;
while (x < mx) {
x = getRLE(img,x,mx,0xff,&run,&code);
if (run < 2) {
if (code != 0xff) {
fputc(code,fp);
}else {
fputc(0xff,fp);
fputc(0x01,fp);
fputc(code,fp);
}
}else if (run == 2) {
if (code != 0xff) {
fputc(code,fp);
fputc(0xff,fp);
}else {
fputc(0xff,fp);
fputc(0x02,fp);
fputc(code,fp);
}
}else {
fputc(0xff,fp);
fputc(run,fp);
fputc(code,fp);
}
}
return 0;
}第二種解壓縮
int decode(FILE *fp) {
int c1;
int run,code;
while (!feof(fp)) {
c1 = fgetc(fp);
if (c1 == EOF) break;
if (c1 == 0xff) {
run = fgetc(fp);
if (run == EOF) break;
code = fgetc(fp);
if (code == EOF) break;
for (int i=0;i<run;i++) {
fputc(code,stdout);
}
}else {
fputc(c1,stdout);
}
}
return 0;
}第三種壓縮
int encode(FILE *fp,byte *img,int mx) {
int run,code;
int x = 0;
while (x < mx) {
x = getRLE(img,x,mx,0x7f,&run,&code);
if (run < 2) {
if (code < 0x80) {
fputc(code,fp);
}else {
fputc(0x81,fp);
fputc(code,fp);
}
}else {
fputc(0x80 | run ,fp);
fputc(code,fp);
}
}
return 0;
}
第三種解壓縮
int decode(FILE *fp) {
int c1;
int run,code;
while (!feof(fp)) {
c1 = fgetc(fp);
if (c1 == EOF) break;
if (c1 > 0x80) {
run = c1 - 0x80; // c1 = run | 0x80
code = fgetc(fp);
if (code == EOF) break;
for (int i=0;i<run;i++) {
fputc(code,stdout);
}
}else {
fputc(c1,stdout);
}
}
return 0;
}利用資料之分布不均勻來做資料壓縮
Huffman Tree
- Huffman Tree本質是利用資料出現的頻率來做壓縮
定義結構
#include <stdio.h>
#include <stdlib.h>
#include <arm/limits.h>
// data define
#define BUFFER_SIZE 1024
#define TRUE 1
// Huffman tree define
#define N 256
#define NODATA 2100000000
#define DEFAULT_MIN (-100)
#define DEFAULT_CODE_SIZE 100
typedef unsigned char byte;
unsigned char buffer[BUFFER_SIZE];公用函數
void encode(FILE *fp,byte *data,int size);
void fputLong(long num, FILE *fp) {
fputc((num >> 24) & 0xff,fp);
fputc((num >> 16) & 0xff,fp);
fputc((num >> 8) & 0xff,fp);
fputc((num) & 0xff,fp);
}
int main(int argc, char **argv) {
if (argc < 3) {
exit(8);
}
FILE *fp_i = fopen(argv[1],"rb");
if (fp_i == NULL) {
fprintf(stderr,"Input file cannot open \n");
exit(8);
}
int i = 0;
int c;
while (i < BUFFER_SIZE && (c=fgetc(fp_i)) != EOF) {
buffer[i] = c;
i++;
}
fclose(fp_i);
FILE *fp_o = fopen(argv[2],"wb");
if (fp_o == NULL) {
fprintf(stderr,"Output file cannot open \n");
exit(8);
}
encode(fp_o,buffer,i);
fclose(fp_o);
return 0;
}
### 定義Huffman tree結構
```c
// Huffman tree array
int l_node[2*N],r_node[2*N];
int parent[2*N];int outputHist(const int *hist,const int nn,FILE *fp) {
for (int i=0;i<nn;i++) {
fputLong(hist[i],fp);
}
return TRUE;
}
void getMin2(const int *hist,const int hm,int *d1,int *d2) {
int min1 = INT_MAX, min2 = INT_MAX;
*d1 = *d2 = DEFAULT_MIN;
for (int i=0;i<hm;i++) {
if (hist[i] != NODATA && hist[i] < min1) {
min1 = hist[i];
*d1 = i;
}
}
for (int i=0;i<hm;i++) {
if (i != *d1 && hist[i] != NODATA && hist[i] < min2) {
min2 = hist[i];
*d2 = i;
}
}
}
int makeTree(int *hist, int n) {
int hm_data = n;
for (int i=0;i < N*2;i ++) {
l_node[i] = r_node[i] = parent[i] = 0;
}
int d1 ,d2;
while (TRUE) {
getMin2(hist,hm_data,&d1,&d2);
if (d1 < 0 || d2 < 0) break;
l_node[hm_data] = d1;
r_node[hm_data] = d2;
parent[d1] = hm_data;
parent[d2] = hm_data;
hist[hm_data] = hist[d1] + hist[d2];
hist[d1] = NODATA;
hist[d2] = NODATA;
hm_data++;
}
return hm_data;
}
static int bits = 0;
static int bdata = 0;
void fputReset() {
bits = 0;
bdata = 0;
}
void fputBit(int bit,FILE *fp) {
bdata = (bdata << 1) | bit;
bits++;
if (bits >= 8 ) {
fputc(bdata,fp);
fputReset();
}
}
void flushBit(FILE *fp) {
if (bits > 0) {
while (bits < 8) {
bdata <<= 1;
bits++;
}
fputc(bdata,fp);
fputReset();
}
}
void outpurEncode(int val,int end,FILE *fp) {
int c = 0;
int code[DEFAULT_CODE_SIZE];
int cur = val;
// 利用樹的可逆性
while (parent[cur] != 0 ) {
int p = parent[cur];
if (l_node[p] == cur) {
code[c++] = 0;
}else if (r_node[p] == cur) {
code[c++] = 1;
}else {
fprintf(stderr,"this node is not belong to parent node \n");
exit(1);
}
cur = p;
}
for (int i = c-1;i >= 0;i--) {
fputBit(code[i],fp);
}
}
void encode(FILE *fp,byte *data,int size) {
int hist[N*2];
for (int i=0;i<N*2;i++) hist[i] = 0;
for (int i=0;i<size;i++) hist[data[i]]++;
fputLong(size,fp);
outputHist(hist,N,fp);
int datas = makeTree(hist,N);
fputReset();
for (int i=0;i<size;i++) {
outpurEncode(data[i],datas,fp);
}
flushBit(fp);
}